Original formulation

From a series of experiments on steady flows of water through filter sands with different grain sizes, Henry Darcy established a relation between the flow $Q$ and the pressure drop $P_2-P_1$:

where $P_1$ and $P_2$ are pressure levels given as manometer heights respectively at the top and the bottom of the sand column. $L$ is the length of the sand column. $K$ is a proportional factor depending on the size and the compactness of the sand grains.

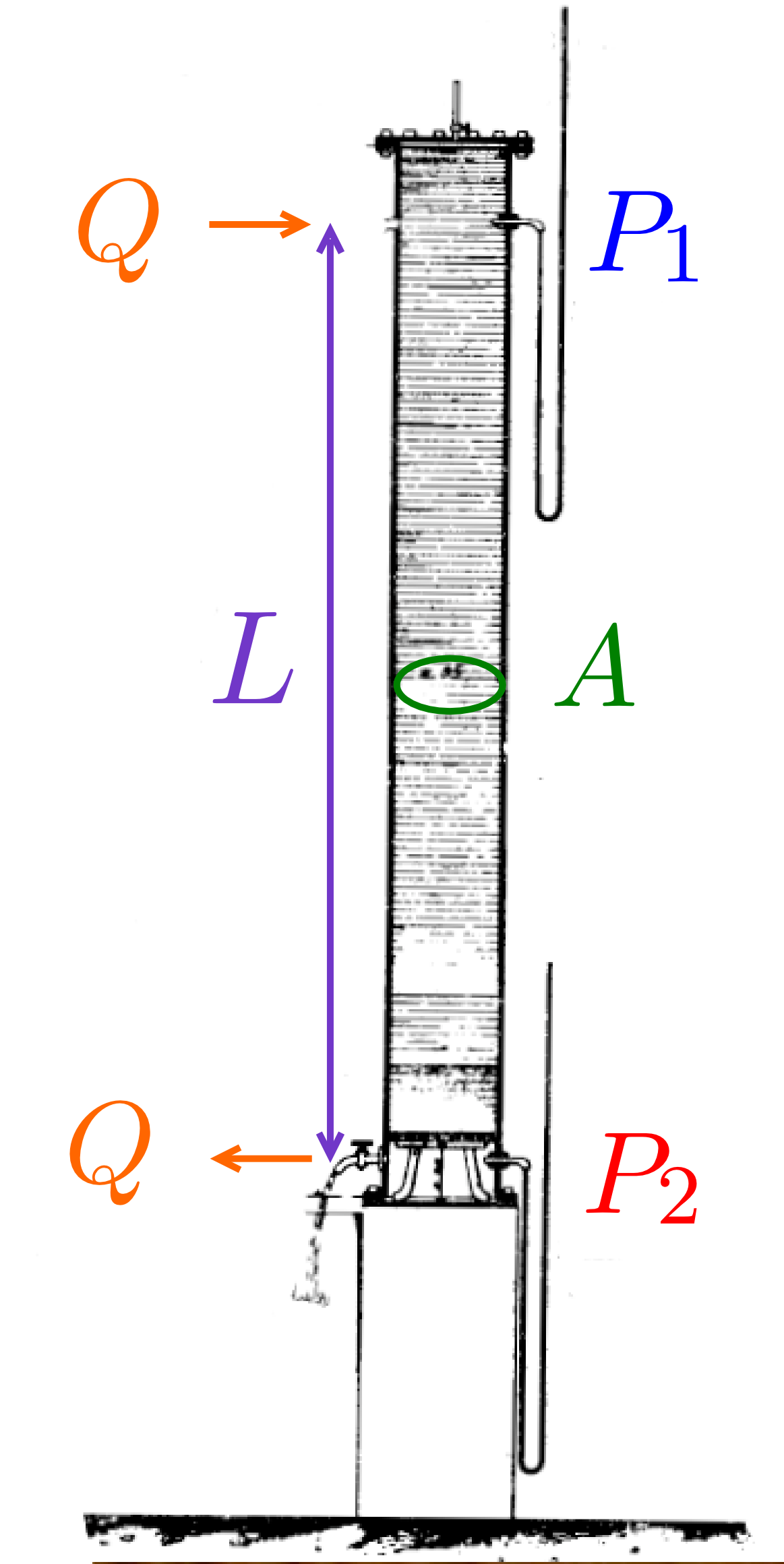
Note that Darcy's equation can be derived from Navier-Stokes equation (see for example the work by M. K. Hubbert presented at Darcy Centennial Hydrology Symposium [Hub56])

Derivative form and implications

Keeping the magnitude of the flow $Q$ to a given value but modifying its direction (upward, downward or oblique...) one measures the same manometer difference $P_2-P_1$. Quoting M. K. Hubbert, this point can be rewritten as:

Darcy's law is invariant with respect to the direction of the flow in the earth's gravity field

This observation leads to a generalization of Darcy's law for flow in the 3D space which can be written in a derivative form and for an isotropic medium as:

where $\phi\vec{v}$ is the fluid flow, $\eta$ is the dynamic viscosity of the fluid, $\rho$ its mass density, $k_{0}$ is the static permeability of the material, $\vec{\nabla}p$ is the pressure gradient and $\vec{g}$ is the gravity vector (the term $-\rho\vec{g}$ is negligible compared to $\vec{\nabla}p$ only in the case of a horizontal flow).

This derivative form of Darcy's work raises the question of how should $\vec{v}$ and $p$ defined ? Should we considere tham as the velocity vector and the pressure at a particular point in the porous material or averaged values over a particular volume of the material ?

Obviously, $\vec{v}$ and $p$ should be consider as averaged value over a Representative Elementary Volume representing the smallest volume on which computation can be done to reproduce the behavior of the material.

Generalization to dynamic regimes

Darcy's law has been extended to the dynamic regime introducing a complex and frequency dependent permeability $k(\omega)$. The homogenization theory justified this generalization a posteriori, see e.g. [Aur80], [ABC85], [Bou00])

where the gravity effect has been neglected.

In 1997, Lafarge & et al. [LLAT97] use a thermal equivalent to the dynamic Darcy's law to describe thermal effects in a porous medium. This work leads to the introduction of a new parameter: the static thermal permeability i.e. the low frequency limit of the thermal permeability.