Mechanical damping
The mechanical damping tends to reduce the amplitude of a vibrating structure
by molecular interactions inside the solid phase of a porous material.
Mainly two models accounting for this damping are used, the
the specific damping, usually characterized with letter
![]() and the hysteretic one, usually characterized by letter
and the hysteretic one, usually characterized by letter
![]() .
.
Hysteretic damping
This model of damping is only defined in Fourier's domain.
|
|
(1) |
dividing eq. (1) by the stiffness of the spring,
![]() ,
leads to the following frequency response (ration of applied force over resulting displacement):
,
leads to the following frequency response (ration of applied force over resulting displacement):

|
(2) |
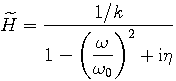
|
(3) |
From this last equation, one can deduce the magnitude of the frequency response:
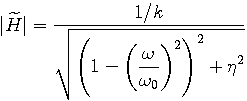
|
(4) |
The resonance angular frequency of the damped system (3),
![]() ,
is obtained solving:
,
is obtained solving:
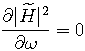
|
(5) |
The left hand side of the previous equation is calculating from eq. (4):
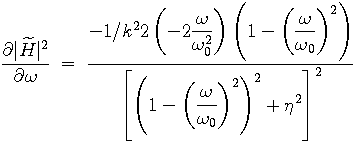
|
(6) |
The right hand side of eq. (6) vanishes when
![]() equals
equals
![]() (for
(for
![]()
![]() ).
).
Thus, the resonance angular frequency of the damped system (3),
![]() ,
is equal to resonance angular frequency of the undamped system
,
is equal to resonance angular frequency of the undamped system
![]() as the driving angular frequency,
as the driving angular frequency,
![]() ,
does not appear in the imaginary part of the frequency response (3).
,
does not appear in the imaginary part of the frequency response (3).
Specific damping
The so-called fundamental equation of the damped harmonic oscillator in the time domain can be written as:
|
|
(7) |
In Fourier's domain, this expression becomes:
|
|
(8) |
From equation (8) the frequency response (ratio of force applied over resulting displacement) is:
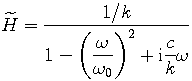
|
(9) |
Introducing the specific damping,
![]() ,
as
,
as
![]() one rewrites eq. (9) as:
one rewrites eq. (9) as:
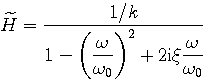
|
(10) |
From eq. (10), the expression of magnitude of the frequency response is deduced:
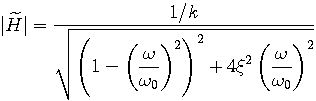
|
(11) |
The resonance angular frequency
![]() is calculated using the same reasoning as for the hysteric case above, i.e. finding
is calculated using the same reasoning as for the hysteric case above, i.e. finding
![]() so that:
so that:
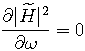
|
(12) |
The left hand side of the previous equation is calculating from eq. (11):
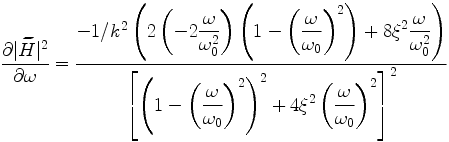
|
(13) |
Except for frequency 0 Hz,
![]() because the driving frequency appears in the imaginary part. With this model, damping appears in the resonance angular frequency.
because the driving frequency appears in the imaginary part. With this model, damping appears in the resonance angular frequency.
Note that
![]() is well defined only for the harmonic oscillator because
is well defined only for the harmonic oscillator because
![]() depends on
depends on
![]() and for a system with multiple freedom degrees
and for a system with multiple freedom degrees
![]() must be defined for each frequency mode.
must be defined for each frequency mode.
Comparison between specific and hysteretic damping
![]() and
and
![]() have both non-dimensional quantities but the two FRF have different behaviours regarding first their resonance frequency.
have both non-dimensional quantities but the two FRF have different behaviours regarding first their resonance frequency.
| Damping model | Magnitude of frequency response |
|---|---|
|
|
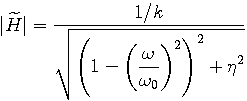
|
|
|
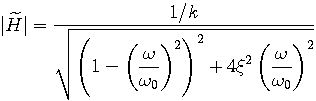
|
At ![]() it is possible to write:
it is possible to write:
| Damping model | Magnitude of frequency response at |
|---|---|
|
|
|
|
|

|
If the two frequency reponses must be the same at
![]() ,
then
,
then
![]() .
This is true at only one frequency.
In practice, these two models are similar for very small damping.
.
This is true at only one frequency.
In practice, these two models are similar for very small damping.
- Comment
- by sending an e-mail to apmr@matelys.com with the current page title.