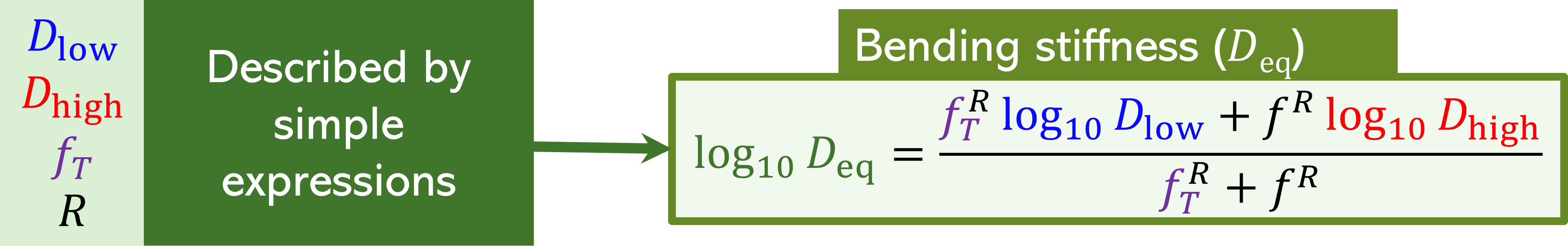APMR
Acoustical Porous Material Recipes

Section: Home | Basics of Mechanics

Condensed models for multilayer structures

In the recent years, structures with multiple layers (for example, fuselage in aircraft, windshield in automotives, glass windows in buildings etc.) are commonly used to enhance sound comfort and noise reduction. Transport and building industries use sandwich constructions which provide higher stiffness and damping while having lighter weight. These solutions are often consist three layers where a soft layer is embedded between two hard skins. While the skins provide the structural stiffness, the soft core helps to increase the energy dissipation.

Condensed models

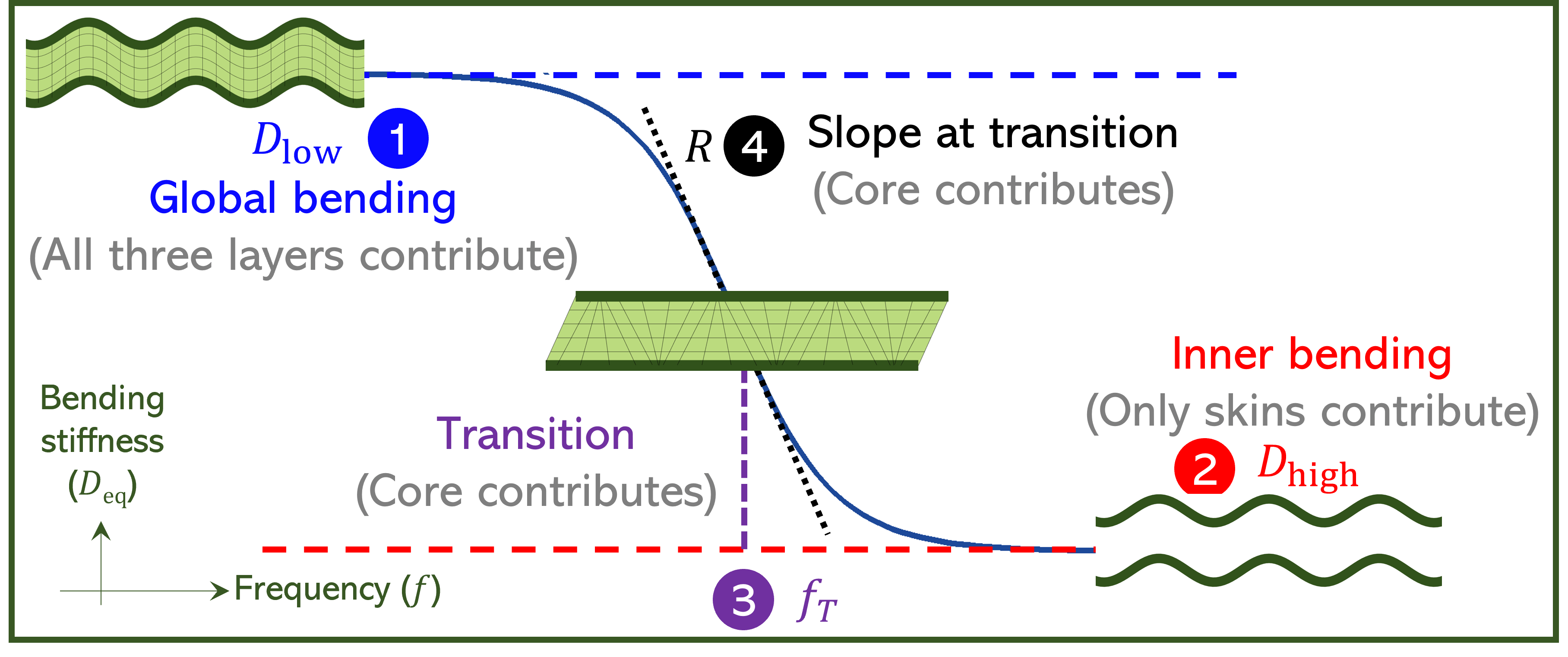
Although there are many different types of models available in the literature to model the behaviour of the multilayer structures, there is one particular type of model that gains attention among various industries and it is called "condensed or equivalent plate models".

The main advantage of condensed models is that it reduces the multilayer structure into a single layer structure, mimicking the same natural behaviour of the actual multilayer structure. By achieving this, it would greatly help us to save or reduce significant amount of computational time and power to compute the vibroacoustic performance quantities (such as transmission loss, absorption coefficient etc.). Condensed models also help to understand physical behaviours of the multilayer system at different frequencies.

Figure 1: Schematic representation of condensed models

In this page, the following two condensed models are discussed:

$\bullet$ Sigmoid model - applicable to three-layer structure of isotropic layers:
(see Arasan U., Marchetti F., Chevillotte F., Jaouen L., Chronopoulos D. and Gourdon E., 2021, "A simple equivalent plate model for dynamic bending stiffness of three-layer sandwich panels with shearing core", Journal of Sound and Vibration, 500, p. 116025. published version or preprint version)

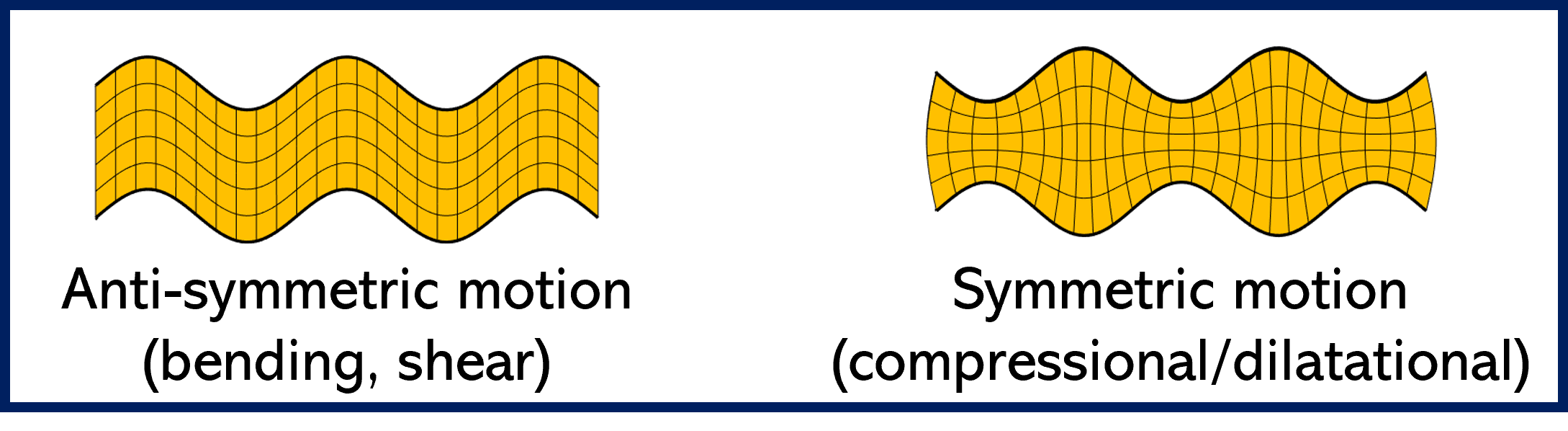
$\bullet$ New condensed model - applicable to symmetric multilayers:
(see Marchetti F., Arasan U., Chevillotte F. and Ege K., 2021, "On the condensation of thick symmetric multilayer panels including dilatational motion", Journal of Sound and Vibration, 502, p. 116078. published version or preprint version)

For more information, you're also invited to look at the recording of Arasan's PhD defense:

Sigmoid model (for three-layer structure)

Although the existing condensed (or equivalent) plate models available in the literature (such as RKU model, Guyader's model etc.), are commonly used across various industries, they often requires some initial work for implementation and/or symbolic computation of solutions from a nonlinear equation which further requires specific techniques to correctly capture the physical behaviour of the system.

Therefore, a simple model is developed to predict the vibroacoustic behaviour a three-layer system which facilitates the implementation process compared to other models. The new model is called as the "Sigmoid model" which computes the equivalent properties of a three-layer structure from its asymptotic behaviours.

Model basics

The sigmoid model is constructed by observing four asymptotic characteristcs of the three-layer structure as shown in Figure 2.
$\bullet$ At low frequencies: a bending behaviour which is controlled by all three layers of the structure (global bending)
$\bullet$ At high frequencies: a bending behaviour which is controlled by only the outer layers of the structure (inner bending)
$\bullet$ At transition frequency: a behaviour which is controlled by the shearing nature of the core layer
$\bullet$ Slope at transition frequency: a characteristic which is controlled by the properties of the core layer

Figure 2: Asymptotic characteristics of a three-layer structure

These four characteristic behaviours of the three-layer structure is discussed well in this journal article. Once these characteristic parameters are calculated, the equivalent property ($D_\text{eq}$) as function of the frequency ($f$) is calculated as shown in Figure 3 below.

Figure 3: Computation of equivalent property from the sigmoid model

New condensed model

The new condensed model, applicable to symmetric multilayers, includes both anti-symmetric and symmetric motions of the multilayer structure whereas other condensed (or equivalent plate) models allow only anti-symmetric motion (including the Sigmoid model).

Figure 4: Two motion types of the structure of infinite extent

Although this model can be applied to symmetric multilayer structure with any number of layers, for the sake of explanation, a three-layer structure is considered here. In this three-layer structure, the core is assumed to be softer than the skins.

Two impedances are needed to fully describe the motions of the structure:
(1) Anti-symmetric impedance ($Z_A$)
(2) Symmetric impedance ($Z_S$) \[ Z_\text{A,eq}=\frac{1}{\text{j}\omega}\left({D}_\text{eq}k_\text{t}^4-\tilde{\rho}_\text{A} h\omega^2\right);\;\;Z_\text{S,eq}=\frac{1}{\text{j}\omega}\left({D}_\text{eq}k_\text{t}^4-\tilde{\rho}_\text{S} h\omega^2\right), \] where $k_t=(\omega/c_0)\sin\theta$ is the transverse wavenumber of the incident wave in air with incidence angle $\theta$ (see Figure 1), $\omega=2\pi f$ is the circular frequency, $h$ is the total thickness of the structure and $\text{j}=\sqrt{-1}$.

Computation of equivalent quantities
$\bullet$ $D_\text{eq}$ - can be computed from any existing equivalent plate model (RKU, Guyader, Sigmoid etc.)
$\bullet$ $\tilde{\rho}_\text{A}$ - average (or mean) density of the multilayer
$\bullet$ $\tilde{\rho}_\text{S}$ - it is computed by assuming the three-layer structure mass-spring-mass system \[ \tilde{\rho}_\text{S}=2\frac{\mathcal{M}}{h}\left(1-\frac{2}{\omega^2\mathcal{C}\mathcal{M}}\right), \] where $\mathcal{M}$ is the mass per unit area of the skin and $\mathcal{C}$ is the compliance of the core layer.

The following interactive application shows the equivalent quantities computed by the Sigmoid model for three-layer symmetric sandwich structure. Properties of these layers could changed below to see their effects on the computed quantities such as $D_\text{eq},\eta_\text{eq},k_\text{eq}$ and transmission loss (TL). The TL is also computed from the new condensed model to compare its accuracy with the Sigmoid model and the Transfer Matrix Method (TMM).

 
Observations:

$\bullet$ $D_\text{low}$ is mainly controlled by the skin properties and core thickness

$\bullet$ Young's modulus of the core $(E_c)$ influences the transition frequnecy $(f_T)$ strongly than other properties

$\bullet$ If the core is too soft (or has low value of Young's modulus $(E_c)$), the new condensed model shows good correspondance with the TMM (in TL computations), whereas the Sigmoid model shows good correspondance only at mass-law region

$\bullet$ If $E_c$ is increased, then the sigmoid model shows good correspondance with the new condensed model as well as with the TMM. This is because the anti-symmetric motions (such as bending, shear) controlls the motion of the structure as the core becomes harder, for which the Sigmoid model is sufficent

Unless otherwise indicated, the content of this page is copyleft under :
the creative commons license Attribution 3.0 Unported (CC BY 3.0),
Arasan Uthayasuryian & Luc Jaouen (@ljaouen), ISSN 2606-4138.
Site hosted by Matelys.