
APMR
Acoustical Porous Material Recipes

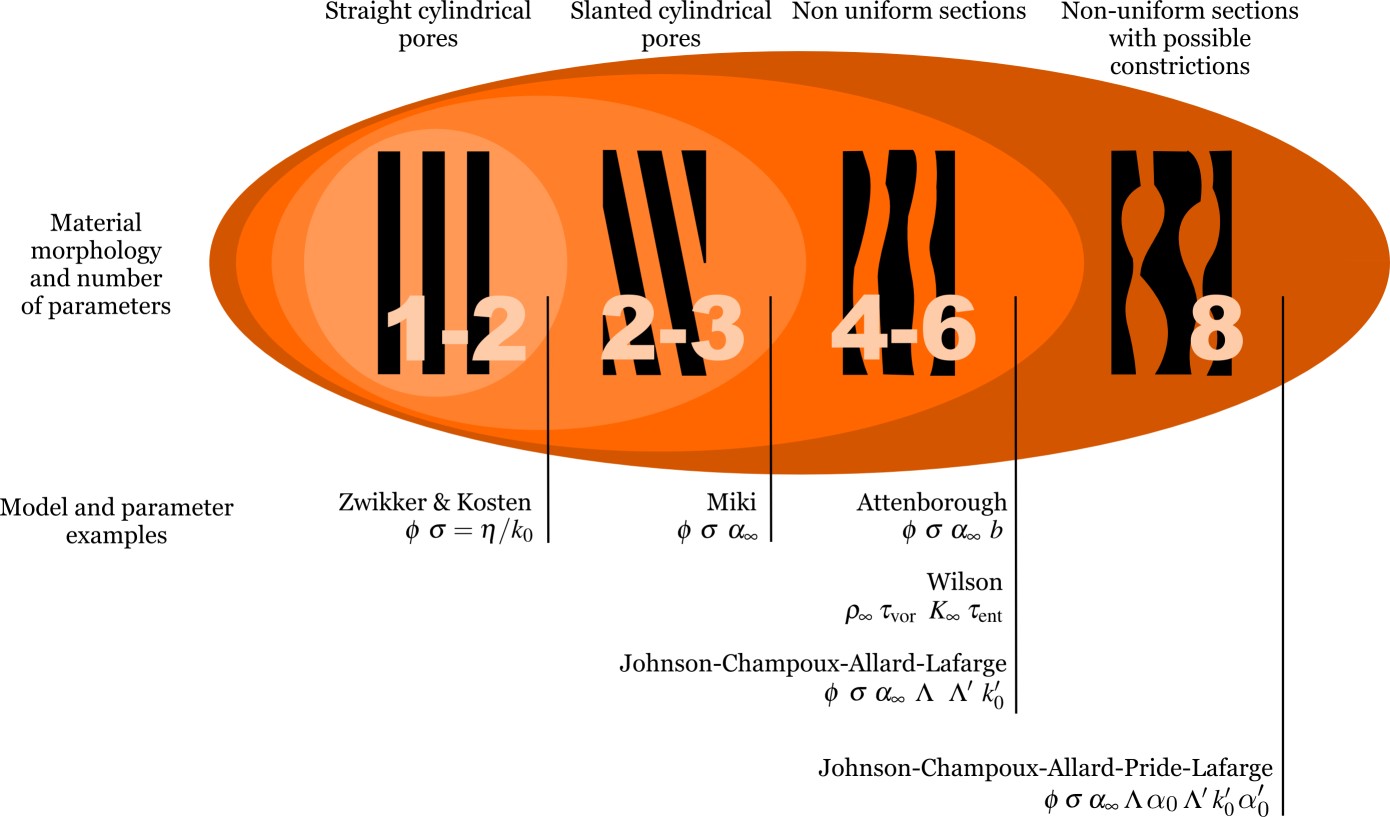
The tables reported below present, for a large number of models, the parameters they require to describe the visco-thermal dissipation effects when sound waves propagate through a porous medium.
This empirical model based on measurements results for fibrous materials should not be used without corrections proposed by Miki (see Delany-Bazley-Miki model below).
| Parameter(s) | Usual notation |
|---|---|
| Static air flow resistivity | $\sigma$ |
This empirical model may be used to described fibrous material behaviors.
| Parameter(s) | Usual notation |
|---|---|
| Static air flow resistivity | $\sigma$ |
The year he published his corrections of Delany-Bazley expressions (1990), Miki also presented a 3-parameter model.
| Parameter(s) | Usual notation |
|---|---|
| Static air flow resistivity | $\sigma$ |
| Open porosity | $\phi$ |
| High frequency limit of the tortuosity | $\alpha_{\infty}$ |
This semi-phenomenological model may be used to described the dissipation behavior of fibrous materials or materials with arbitrary pore shapes without important pore section variations.
| Parameter(s) | Usual notation |
|---|---|
| Static air flow resistivity | $\sigma$ |
| Open porosity | $\phi$ |
| High frequency limit of the tortuosity | $\alpha_{\infty}$ |
| Viscous characteristic length | $\Lambda$ |
| Thermal characteristic length | $\Lambda'$ |
This semi-phenomenological model may be used to described the dissipation behavior of materials with arbitrary pore shapes without important pore section variations.
| Parameter(s) | Usual notation |
|---|---|
| Static air flow resistivity | $\sigma$ |
| Open porosity | $\phi$ |
| High frequency limit of the tortuosity | $\alpha_{\infty}$ |
| Viscous characteristic length | $\Lambda$ |
| Thermal characteristic length | $\Lambda'$ |
| Static thermal permeability | $k'_{0}$ |
This semi-phenomenological model may be used to described the dissipation behavior of materials with arbitrary pore shapes and important pore section variations.
| Parameter(s) | Usual notation |
|---|---|
| Static air flow resistivity | $\sigma$ |
| Open porosity | $\phi$ |
| High frequency limit of the tortuosity | $\alpha_{\infty}$ |
| Viscous characteristic length | $\Lambda$ |
| Thermal characteristic length | $\Lambda'$ |
| Static thermal permeability | $k'_{0}$ |
| Static viscous tortuosity | $\alpha_0$ |
| Static thermal tortuosity | $\alpha_0'$ |
This semi-phenomenological model may be used to described the dissipation behavior of fibrous materials or materials with arbitrary pore shapes without important pore section variations.
| Parameter(s) | Usual notation |
|---|---|
| High frequency limit of the dynamic density | $\rho_{\infty}$ |
| Vorticity-mode relaxation time | $\tau_{\textrm{vor}}$ |
| High frequency limit of the bulk modulus | $K_{\infty}$ |
| Entropy-mode relaxation time | $\tau_{\textrm{ent}}$ |