Visco-inertial effects

In 1987, Johnson Koplik and Dashen [JKD87] proposed a semi-phenomenological model to describe the complex density of an acoustical porous material with a motionless skeleton having arbitrary pore shapes. This expression is:

\[ \widetilde{\rho}(\omega) = \frac{ \alpha_{\infty} \rho_{0} }{ \phi } \Bigg[ 1 + \frac{ \sigma \phi }{ j \omega \rho_{0} \alpha_{\infty}} \sqrt{ 1 + j\frac{ 4 \alpha_{\infty}^{2} \eta \rho_{0} \omega }{ \sigma^{2} \Lambda^{2} \phi^{2}} }\Bigg] \]

4 parameters are involved in the calculation of this dynamic density: the open porosity $\phi$, the static air flow resistivity $\sigma$, the high frequency limit of the tortuosity $\alpha_{\infty}$ and the viscous characteristic length $\Lambda$.

As reported in the section limitations, the low frequency limit of the real part of the dynamic mass density expression is not exact.

Thermal effects

In 1991, Champoux & Allard [CA91] introduced an expression for the dynamic bulk modulus for the same kind of porous material based on the previous work by Johnson et al. This work, in addition to the work by Jonhson et al. described above lead to the definition the Johnson-Champoux-Allard model.
The expression of $\widetilde{K}$ given by Champoux & Allard is then modified in 1993 by Lafarge et al. [LLAT97] which highlight a lack of information at low frequencies for thermal effects.
Indeed, four parameters are required to compute $\widetilde{\rho}$ from Johnson et al. work and describe the visco-inertial effects while only two parameters are used to compute $\widetilde{K}$ and describe the thermal effects from Champoux & Allard work.

This observation leads Lafarge et al. to introduce a new parameter, the static thermal permeability $k'_{0}$, in order to describe the low frequency behavior of thermal effects.

The new model for $\widetilde{K}$ introduced by Lafarge et al. is :

\[ \widetilde{K}(\omega) = \displaystyle{\frac{\gamma P_{0}/\phi} {\gamma - (\gamma-1) \left[ 1-j\displaystyle{\frac{\phi\kappa} {k'_0 C_p\rho_{0}\omega}} \sqrt{ 1+j \displaystyle{\frac{4{k'}_{0}^{2} C_p\rho_{0}\omega} {\kappa\Lambda'^2\phi^2}} } \, \right]^{-1} }} \]

3 parameters are involved in the calculation of this dynamic bulk modulus: the open porosity $\phi$, the thermal characteristic length $\Lambda'$ and the static thermal permeability $k'_0$.

Limitation

Wrong low frequency limits

The expression of $\widetilde{\rho}$ given by Johnson, Koplik & Dashen does not describe the exact behavior of the dynamic mass density as $\omega$ tends to zero. The real part of the mass density (or the imaginary part of the dynamic permeability) is not correct.

Similarly, the expression of $\widetilde{K}$ given by Champoux & Allard and further modified by Lafarge et al. is not correct at low frequencies. [I know I have to develop this part. Give me some time to do so.]

Pride, Morgan & Gangi [PMG93] have proposed a modified expression of the dynamic density. However, the expression given by Pride, Morgan & Gangi and further modified by D. Lafarge [Laf93] is rarely used as the new required parameters need developments to be characterized.

Changes to the JCA model by Pride et al. and D. Lafarge are detailed in the Johnson-Champoux-Allard-Pride-Lafarge model.

Computation

of the sound absorption coefficient

The figure presents the sound absorption coefficients (plane waves at normal incidence and diffuse sound field) of

• a mm-thick porous material backed by a rigid and impermeable wall with
• a porosity of %,
• a static air-flow resistivity of N.s.m$^{-4}$,
• a high frequency limit of the dynamic tortuosity ,
• a viscous characteristic length of microns,
• a thermal characteristic length of microns.
• a static thermal permeability of 10$^{-10}$ m$^2$.

Click/Touch and drag the underlined blue text to change the values and compute a new result.


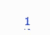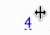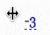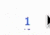
There is no consistency check of the parameters in these simulations.

Sound abs. coefficient vs. frequency:

■: plane waves at normal incidence, ■: diffuse field.